Table of Contents

Basic Python: Operators

Operator Name Description
a + b Addition Sum of a and b
a - b Subtraction Difference of a and b
a * b Multiplication Product of a and b
a / b True division Quotient of a and b
a // b Floor division Quotient of a and b, removing fractional parts
a % b Modulus Integer remainder after division of a by b
a ** b Exponentiation a raised to the power of b
-a Negation The negative of a
+a Unary plus a unchanged (rarely used)
In [1]:
# addition, subtraction, multiplication
print((4 + 8) * (6.5 - 3))

42.0
In [2]:
# Division
print(11 / 2)

5.5

Assignment Operations

In [3]:
a = 24
print(a)

24
In [4]:
a = a + 2
print(a)

26
In [5]:
print(a + 2)

28
In [6]:
a += 2  # equivalent to a = a + 2
print(a)

28

Comparison Operations

Operation Description
a == b a equal to b
a < b a less than b
a <= b a less than or equal to b
a != b a not equal to b
a > b a greater than b
a >= b a greater than or equal to b
In [7]:
print(22 / 2 == 10 + 1)

True
In [8]:
# 25 is even
print(25 % 2 == 0)

False
In [9]:
# 66 is odd
print(66 % 2 == 0)

True
In [10]:
# check if a is between 15 and 30
a = 25
print(15 < a < 30)

True

Boolean Operations

In [11]:
x = 4
print((x < 6) and (x > 2))

True
In [12]:
print((x > 10) or (x % 2 == 0))

True
In [13]:
print(not (x < 6))

False

Membership Operators

Operator Description
a in b True if a is a member of b
a not in b True if a is not a member of b
In [14]:
print(1 in [1, 2, 3])

True
In [15]:
print(2 not in [1, 2, 3])

False

Built-In Types

Type Example Description
int x = 1 integers (i.e., whole numbers)
float x = 1.0 floating-point numbers (i.e., real numbers)
complex x = 1 + 2j Complex numbers (i.e., numbers with real and imaginary part)
bool x = True Boolean: True/False values
str x = 'abc' String: characters or text
NoneType x = None Special object indicating nulls

Integers

In [16]:
5 / 2
Out[16]:
2.5
In [17]:
# Floor division
5 // 2
Out[17]:
2

The floor division operator was added in Python 3; you should be aware if working in Python 2 that the standard division operator (/) acts like floor division for integers and like true division for floating-point numbers.

Floating-Point Numbers

In [18]:
x = 0.000005
y = 5e-6
print(x == y)

True
In [19]:
print(0.1 + 0.2 == 0.3)

False

Floating-point precision is limited, which can cause equality tests to be unstable

String Type

In [20]:
message = "what do you like?"
print(message)

what do you like?
In [21]:
response = 'spam'
print(response)

spam
In [22]:
# length of string
print(len(response))

4
In [23]:
# Make upper-case. See also str.lower()
print(response.upper())

SPAM
In [24]:
# Capitalize. See also str.title()
print(message.capitalize())

What do you like?
In [25]:
# concatenation with +
print(message + response)

what do you like?spam
In [26]:
# multiplication is multiple concatenation
print(5 * response)

spamspamspamspamspam
In [27]:
# Access individual characters (zero-based indexing)
print(message[0])

w
In [28]:
# index range is checked
print(message[59])

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-28-ecd28c2b2692> in <module>
      1 # index range is checked
----> 2 print(message[59])

IndexError: string index out of range
In [29]:
a = 32423
print('el valor de a es ', a)

el valor de a es  32423
In [30]:
print(f'a vale {a}')

a vale 32423

valor = input('introduce una cadena')
print('la candena introducida es ', valor)

Boolean Type

In [31]:
result = (4 < 5)
print(result)

True

True and False must be capitalized!

Exercises

  • How many hours are in a year?
  • How many minutes are in a decade?
  • How many seconds old are you?

Leap years can be ignored

In [32]:
# How many hours are in a year?
In [33]:
print(24 * 365)

8760
In [34]:
# How many minutes are in a decade?
In [35]:
print(60 * 24 * (365 * 10))

5256000
In [36]:
# How many seconds old are you?
In [37]:
print(60 * 60 * 24 * (365 * 23))

725328000

Built-In Data Structures

Type Name Example Description
list [1, 2, 3] Ordered collection
tuple (1, 2, 3) Immutable ordered collection
dict {'a': 1, 'b': 2, 'c': 3} Unordered (key,value) mapping (ordered in Python 3.7+)
set {1, 2, 3} Unordered collection of unique values

Lists

In [38]:
l = [2, 3, 5, 7]
In [39]:
# Length of a list
print(len(l))

4
In [40]:
# Append a value to the end
l.append(11)
print(l)

[2, 3, 5, 7, 11]
In [41]:
# Addition concatenates lists
print(l + [13, 17, 19])

[2, 3, 5, 7, 11, 13, 17, 19]
In [42]:
# sort() method sorts in-place
l = [2, 5, 1, 6, 3, 4]
l.sort()
print(l)

[1, 2, 3, 4, 5, 6]
In [43]:
l = [1, 'two', 3.14, [0, 3, 5]]
print(l)

[1, 'two', 3.14, [0, 3, 5]]

List indexing and slicing

In [44]:
l = [2, 3, 5, 7, 11]
In [45]:
print(l[0])

2
In [46]:
print(l[1])

3
In [47]:
print(l[-1])

11

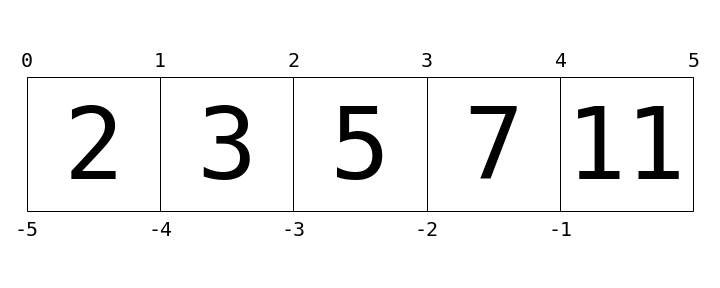
List Indexing Figure

In [48]:
print(l[0:3])

[2, 3, 5]
In [49]:
print(l[:3])

[2, 3, 5]
In [50]:
print(l[::2])  # equivalent to l[0:len(l):2]

[2, 5, 11]
In [51]:
l[0] = 100
print(l)

[100, 3, 5, 7, 11]

Tuples

In [52]:
t = (1, 2, 3)
print(t)

(1, 2, 3)
In [53]:
t = 1, 2, 3
print(t)

(1, 2, 3)
In [54]:
print(len(t))

3
In [55]:
print(t[0])

1
In [56]:
t[1] = 4

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-56-87b0f225887f> in <module>
----> 1 t[1] = 4

TypeError: 'tuple' object does not support item assignment
In [57]:
t.append(4)

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
<ipython-input-57-ada7ed8a579e> in <module>
----> 1 t.append(4)

AttributeError: 'tuple' object has no attribute 'append'

Dictionaries

In [58]:
numbers = {'one': 1, 'two': 2, 'three': 3}
In [59]:
# Access a value via the key
print(numbers['two'])

2
In [60]:
# Set a new key:value pair
numbers['ninety'] = 90
print(numbers)

{'one': 1, 'two': 2, 'three': 3, 'ninety': 90}
In [61]:
numbers = {'one': 1, 'two': 2, 'three': 3}

Exercises

  • Create a dictionary with the following birthday information:
  • Albert Einstein - 03/14/1879
  • Benjamin Franklin - 01/17/1706
  • Ada Lovelace - 12/10/1815
  • Donald Trump - 06/14/1946
  • Rowan Atkinson - 01/6/1955
  • Check if Donald Trump is in our dictonary
  • Get Albert Einstein's birthday
In [62]:
# Create a dictionary with the following birthday information
In [63]:
birthdays = {'Albert Einstein': '03/14/1879',
             'Benjamin Franklin': '01/17/1706',
             'Ada Lovelace': '12/10/1815',
             'Donald Trump': '06/14/1946',
             'Rowan Atkinson': '01/6/1955'}
In [64]:
# Check if Donald Trump is in our dictonary
In [65]:
print('Donald Trump' in birthdays)

True
In [66]:
# Get Albert Einstein's birthday
In [67]:
print(birthdays['Albert Einstein'])

03/14/1879

Control Flow

Conditional Statements: if-elif-else

In [68]:
x = -15

if x == 0:
    print(x, 'is zero')
elif x > 0:
    print(x, 'is positive')
else:
    print(x, 'is negative')

-15 is negative

Loops: for

In [69]:
n = [2, 3, 5, 7]
for e in n:
    print(e)

2
3
5
7
In [70]:
m = range(5)  # m = [0, 1, 2, 3, 4]
for i in m:
    print('hola')

hola
hola
hola
hola
hola

Please avoid Matlab-like for statements with range

In [71]:
n = [2, 3, 5, 7]
for e in range(len(n)):
    print(n[e])

2
3
5
7
In [72]:
for a in n[:3]:
    print(a)

2
3
5

Loops: while

In [73]:
i = 0
while i < 10:
    print(i)
    i += 1

0
1
2
3
4
5
6
7
8
9

Be careful with while loops

Functions

Defining Functions

In [74]:
import time

def cabecera():
    mensaje = 'Este programa está escrito por Juan Gómez'
    mensaje += '. Copyright ' + time.strftime('%d-%m-%Y')
    
    return mensaje

print(cabecera())

Este programa está escrito por Juan Gómez. Copyright 22-11-2018
In [75]:
def cabecera_mejorada(autor):
    mensaje = 'Este programa está escrito por '
    mensaje += autor
    mensaje += '. Copyright ' + time.strftime('%d-%m-%Y')
    
    return mensaje

print(cabecera_mejorada('Juan Gómez'))

Este programa está escrito por Juan Gómez. Copyright 22-11-2018
In [76]:
print(cabecera_mejorada('Alfonso Hernández'))

Este programa está escrito por Alfonso Hernández. Copyright 22-11-2018
In [77]:
def fibonacci(n):
    l = []
    a = 0
    b = 1
    while len(l) < n:
        l.append(a)
        c = a + b
        a = b
        b = c
    return l
In [78]:
print(fibonacci(10))

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
In [79]:
print(fibonacci(3))

[0, 1, 1]

Default Argument Values

In [80]:
def fibonacci(n, start=0):
    l = []
    a = 0
    b = 1
    while len(l) < n:
        if a >= start:
            l.append(a)
        c = a + b
        a = b
        b = c
    return l
In [81]:
print(fibonacci(10))

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
In [82]:
print(fibonacci(10, 5))

[5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
In [83]:
## Keyword arguments
In [84]:
print(fibonacci(start=5, n=10))

[5, 8, 13, 21, 34, 55, 89, 144, 233, 377]

Documentation strings (docstrings)

  • Python documentation strings (docstrings) provide a convenient way of associating documentation with Python functions and modules.
  • Docstrings can be written following several styles. We use Google Python Style Guide.
  • An object's docsting is defined by including a string constant as the first statement in the function's definition.
  • Unlike conventional source code comments the docstring should describe what the function does, not how.
  • All functions should have a docstring.
  • This allows to inspect these comments at run time, for instance as an interactive help system, or export them as HTML, LaTeX, PDF or other formats.
In [85]:
def fibonacci(n, start=0):
    """Build a Fibonacci series with n elements starting at start

    Args:
        n: number of elements
        start: lower limit. Default 0

    Returns:
        A list with a Fibonacci series with n elements
    """
    l = []
    a = 0
    b = 1
    while len(l) < n:
        if a >= start:
            l.append(a)
        c = a + b
        a = b
        b = c
    return l

Exercises

  • Reverse a string

Example input: "cool" output: "looc"

  • Calculate the Hamming difference between two DNA strands

A mutation is simply a mistake that occurs during the creation or copying of a nucleic acid, in particular DNA.

Because nucleic acids are vital to cellular functions, mutations tend to cause a ripple effect throughout the cell.

Although mutations are technically mistakes, a very rare mutation may equip the cell with a beneficial attribute.

In fact, the macro effects of evolution are attributable by the accumulated result of beneficial microscopic mutations over many generations.

The simplest and most common type of nucleic acid mutation is a point mutation, which replaces one base with another at a single nucleotide.

By counting the number of differences between two homologous DNA strands taken from different genomes with a common ancestor, we get a measure of the minimum number of point mutations that could have occurred on the evolutionary path between the two strands.

This is called the 'Hamming distance'.

It is found by comparing two DNA strands and counting how many of the nucleotides are different from their equivalent in the other string.

Example:

GAGCCTACTAACGGGAT

CATCGTAATGACGGCCT

^ ^ ^ ^ ^ ^^

  • Given a number, determine if it is prime

  • Given a number, determine what the nth prime is

In [86]:
# Reverse a string
In [87]:
cadena1 = 'cool'
cadena2 = ''
for c in cadena1[-1::-1]:
    cadena2 = cadena2 + c
print(cadena2)

looc
In [88]:
cadena1 = 'hola mundo'
cadena2 = ''
for c in cadena1[-1::-1]:
    cadena2 = cadena2 + c
print(cadena2)

odnum aloh
In [89]:
cadena = 'cool'

def invertir_cadena(cadena_entrada):
    cadena_salida = ''
    for c in cadena_entrada[-1::-1]:
        cadena_salida += c
    return cadena_salida

print(invertir_cadena(cadena))

looc
In [90]:
print(invertir_cadena('Hola mundo'))

odnum aloH
In [91]:
# Hamming distance
In [92]:
c1 = 'GAGCCTACTAACGGGAT'
c2 = 'CATCGTAATGACGGCCT'

def hamming(dna_1, dna_2):
    l = len(dna_1)
    hamming = 0
    for i in range(l):
        if dna_1[i] != dna_2[i]:
            hamming += 1
    return hamming

print(hamming(c1, c2))

7
In [93]:
print(hamming('TAGAG', 'TAGAA'))

1
In [94]:
# Prime number
In [95]:
number = 4

def is_prime(number):
    is_prime = True
    for x in range(2, number):
        if (number % x) == 0:
            is_prime = False
    return is_prime

is_prime(number)
Out[95]:
False
In [96]:
# Nth Prime
In [97]:
def n_prime(nth):
    n = 2
    primes = []
    while len(primes) < nth:
        if is_prime(n):
            primes.append(n)
        n += 1
    return primes[-1]

print(n_prime(6))

13
In [115]:
print(n_prime(1))

2

Modules and Packages

Loading Modules: the import Statement

Explicit module import

In [98]:
import functions  # without .py extension
print(functions.fibonacci(5))

[0, 1, 1, 2, 3]

Explicit module import by alias

In [99]:
import functions as f
print(f.fibonacci(5))

[0, 1, 1, 2, 3]

Explicit import of module contents

In [100]:
from functions import fibonacci
print(fibonacci(5))

[0, 1, 1, 2, 3]

Importing from Third-Party Modules

The best way to import libraries is included in their official help

import math
import numpy as np
from scipy import linalg, optimize
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import sympy

Code Style

  • Style Guide for Python Code: PEP8.
  • Use only English (ASCII) characters for variables, functions and files.
  • Name your variables, functions and files consistently: the convention is to use lower_case_with_underscores.
  • We all use single-quoted strings to be consistent. Nevertheless, single-quoted strings and double-quoted strings are the same. PEP does not make a recommendation for this, except for function documentation where tripe-quote strings should be used.

PEP8 exceptions

  • Long lines

It is very conservative and requires limiting lines to 79 characters. We use all lines to a maximum of 119 characters. This is the default behaviour in PyCharm.

  • Disable checks in one line

Skip validation in one line by adding following comment:

# nopep8

Data Science Tools

NumPy: Numerical Python

In [101]:
import numpy as np
x = np.arange(1, 10)
print(x)

[1 2 3 4 5 6 7 8 9]
In [102]:
print(x ** 2)

[ 1  4  9 16 25 36 49 64 81]
In [103]:
y = x.reshape((3, 3))
y
Out[103]:
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
In [104]:
print(y.T)

[[1 4 7]
 [2 5 8]
 [3 6 9]]
In [105]:
a = np.array([[1, 0], [0, 1]])
b = np.array([[4, 1], [2, 2]])

print(np.dot(a, b))

[[4 1]
 [2 2]]

Vectorization

Arrays enable you to express batch operations on data without writing any for loops. This is usually called vectorization:

  • vectorized code is more concise and easier to read
  • fewer lines of code generally means fewer bugs
  • the code more closely resembles standard mathematical notation

But:

sometimes it's difficult to move away from the for-loop school of thought

Pandas: Labeled Column-oriented Data

  • fast and efficient Series (1-dimensional) and DataFrame (2-dimensional) heterogeneous objects for data manipulation with integrated indexing
  • tools for reading and writing data from different formats: CSV and text files, Microsoft Excel, SQL databases, HDF5...
  • intelligent label-based slicing
  • time series-functionality
  • integrated handling of missing data
In [106]:
import pandas as pd
df = pd.DataFrame({'label': ['A', 'B', 'C', 'A', 'B', 'C'],
                   'value': [1, 2, 3, 4, 5, 6]})
print(df)

  label  value
0     A      1
1     B      2
2     C      3
3     A      4
4     B      5
5     C      6
In [107]:
print(df['label'])

0    A
1    B
2    C
3    A
4    B
5    C
Name: label, dtype: object
In [108]:
print(df['value'].sum())

21
In [109]:
print(df.groupby('label').sum())

       value
label       
A          5
B          7
C          9

Matplotlib scientific visualization

In [110]:
import matplotlib.pyplot as plt
In [111]:
x = np.linspace(0, 10)  # range of values from 0 to 10
y = np.sin(x)           # sine of these values
plt.plot(x, y);         # plot as a line

SciPy: Scientific Python

  • scipy.fftpack: Fast Fourier transforms
  • scipy.integrate: Numerical integration
  • scipy.interpolate: Numerical interpolation
  • scipy.linalg: Linear algebra routines
  • scipy.optimize: Numerical optimization of functions
  • scipy.sparse: Sparse matrix storage and linear algebra
  • scipy.stats: Statistical analysis routines

Sympy: Symbolic Python

In [112]:
from IPython.display import display
from sympy import symbols

# Pretty printing
from sympy import init_printing
init_printing()

x, y = symbols('x y')
expr = x + 2*y

display(expr)
$$x + 2 y$$

Derivative of $$sin(x)e^x$$

In [113]:
from sympy import diff, sin, exp, pprint

out = diff(sin(x)*exp(x), x)

display(out)
$$e^{x} \sin{\left (x \right )} + e^{x} \cos{\left (x \right )}$$

Compute $$\int(e^x\sin{(x)} + e^x\cos{(x)})\,dx$$

In [114]:
from sympy import integrate, cos

out = integrate(exp(x) * sin(x) + exp(x) * cos(x), x)

display(out)
$$e^{x} \sin{\left (x \right )}$$